Rango de una matriz por el método de Gauss
Explico y resuelvo dos ejercicios en los que calculo el rango por el método de Gauss. El rango es el número de filas o columnas linealmente independientes. Primero hago la matriz escalonada con ceros debajo de la diagonal principal y a continuación observo el número de filas no nulas. El rango será el número de filas distintas de cero.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
Matriz INVERSA por el método de Gauss Jordan
Calculo la inversa por el método de Gauss Jordan. Cuidado porque no siempre se puede calcular la inversa de una matriz. En el segundo ejemplo el rango es menor que el orden y no existe la inversa.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
Si B es la matriz inversa de A, ¿cuánto vale K? Definición de matriz inversa.
Aplico la definición de matriz inversa para calcular el valor del prámetro K.
Multiplico la matriz A por su inversa para obtener la matriz identidad de orden 3X3.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
Si la matriz tiene inversa, ¿Cuánto vale K?
Una matriz cuadrada de orden n tiene inversa, si y sólo si el rango de la matriz es igual a n.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
DEMUESTRA que esta matriz es ORTOGONAL
Una matriz cuadrada es ortogonal si su inversa coincide con su traspuesta.
Para hacer la demostración compruebo que el producto de la matriz A por su traspuesta da la identidad porque esa es la dedinición de inversa. El producto de una matriz por su inversa da la identidad, luego si quiero comporbar que la traspuesta es la inversa, al multiplicar se comportará igual y también obtendré la identidad.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
Si la matriz es ortogonal, calcula x e y
Una matriz cuadrada es ortogonal si su inversa coincide con su traspuesta.
Para calcular x e y aplico que el producto de la matriz A por su traspuesta da la identidad porque esa es la definición de inversa. El producto de una matriz por su inversa da la identidad, luego si quiero que se cumpla que la traspuesta es la inversa, al multiplicar se comportará igual y también obtendré la identidad.
(pincha aquí para ver en YouTube)
Shorts de ejercicios:
Hay muchos mas ejercicios así, búscalos entre los vídeos.
Ecuación matricial: Calcula X (matrices 2×2)
Resuelvo una ecuación con matrices. Primero despejo el valor de X. Cuidado porque el producto de matrices no conmuta. El cálculo de inversa lo hago por el método de Gauss Jordan.
(pincha aquí para ver en YouTube)
Determinante de una matriz de orden 3X3. Ejemplos regla de Sarrus.
Calculo el determinante de dos matrices de orden 3X3 una de ellas con parámetro.
(pincha aquí para ver en YouTube)
Matriz INVERSA con parámetros
Explico qué es la matriz inversa y calculo el parámetro m para que dos matrices A y B sean una la inversa de la otra.
(pincha aquí para ver en YouTube)
¿LO SABES? Si A es una matriz no nula, ¿puede ser nula A^2?
Resuelvo este dilema…………. poniendo un ejemplo para comprobar que efectivamente, el cuadrado de una matriz no nula puede ser nulo.
(pincha aquí para ver en YouTube)
Identidad notable con MATRICES: suma por diferencia NO es diferencia de cuadrados
Explico por qué con matrices NO se cumple la identidad notable: suma por diferencia igual al cuadrado del primero menos el cuadrado del segundo.
(pincha aquí para ver en YouTube)
Calcula la matriz X que cumple la igualdad
Calculo la matriz que cumple la ecuación.
(pincha aquí para ver en YouTube)
RANGO en función de un PARÁMETRO por Gauss y con determiantes.
Estudio el rango de una matriz en función de un parámetro por dos métodos diferentes.
(pincha aquí para ver en YouTube)
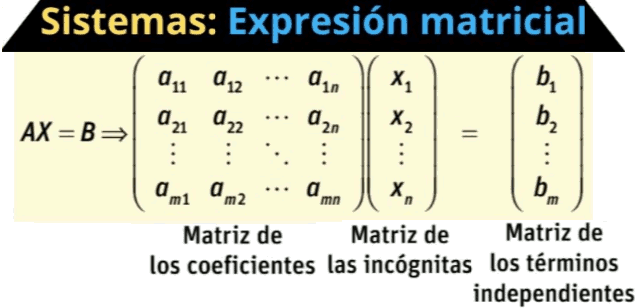
PRODUCTO de MATRICES: orden, mat fila por mat columna, producto en general, propiedades y ejemplos
Explico el producto de dos matrices: dimensiones, teoría y ejemplo del producto de matriz fila por matriz columna, producto en general de dos matrices de cualquier tamaño y propiedades (destacando que el producto no conmuta). Todo ello con ejercicios explicados paso a paso.
(pincha aquí para ver en YouTube)
TRANSFORMACIONES que conservan el RANGO de una MATRIZ.
Explico qué es el rango, qué es una combinación lineal y qué transformaciones se pueden hacer sobre una matriz de forma que la matriz equivalente obtenida conserve el rango. Hay muchos ejemplos acompañando la explicación.
(pincha aquí para ver en YouTube)
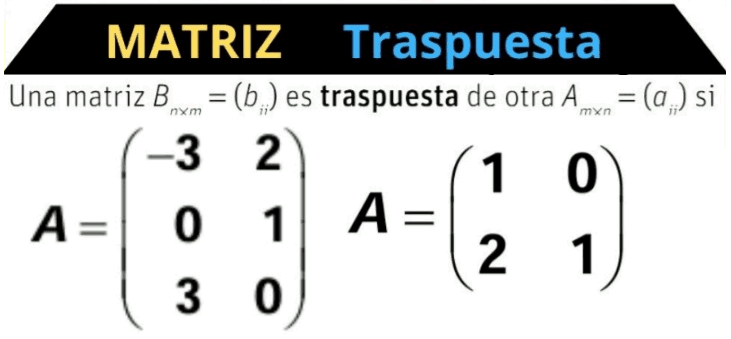
QUÉ ES una matriz y diferentes tipos (CLASIFICACIÓN)
Explico qué es una matriz, su nomenclatura y su clasificación: matriz nula, matriz fila, matriz columna, matrices iguales, matriz traspuesta, triangular superior, triangular inferior, matriz diagonal, escalar, matriz identidad.
(pincha aquí para ver en YouTube)
Ecuación con DETERMINANTE 4×4
Calculo el determinante 4×4 por el método de recurrencia utilizando adjuntos para despúes calcular x en la ecuación resultante.
(pincha aquí para ver en YouTube)
Cómo Despejar la Matriz X en Ecuaciones Matriciales | Ejemplos Resueltos Desde Nivel Básico hasta Avanzado
En este video de Lógica y Mente te explico paso a paso cómo despejar la matriz X en ecuaciones matriciales, ideal para estudiantes de Bachillerato y aquellos que se preparan para los exámenes EBAU/PAU. Comienzo con ejemplos básicos y avanzo hasta problemas más complejos, cubriendo cada nivel de dificultad para que entiendas todo a la perfección.
(pincha aquí para ver en YouTube)
Ecuaciones matriciales resueltas paso a paso | Matemáticas fáciles para EBAU y Bachillerato
En este video, te enseño cómo resolver ecuaciones matriciales paso a paso, de forma sencilla y clara. Aprenderás todo lo necesario para manejar este tema clave en matemáticas, desde el nivel básico hasta avanzado.
(pincha aquí para ver en YouTube)
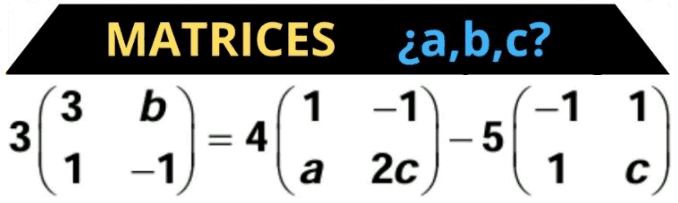
Cálculo con MATRICES (Tipo PAU)
En este video resuelvo paso a paso una ejercicio en el que calculo los parámetros para que se cumpla la ecuación matricial dada de dato. Partimos de la ecuación matricial dada y aplicamos propiedades básicas de las matrices, como operaciones de suma y producto, hasta llegar a los valores de los parámetros desconocidos.
Este tipo de ejercicios es muy útil para reforzar conceptos de álgebra matricial y suele aparecer en exámenes de nivel avanzado, como EBAU o Bachillerato. ¡Aprende conmigo y domina las ecuaciones matriciales de manera sencilla!
(pincha aquí para ver en YouTube)
Ecuación con determinante
Ecuación con determinante
(pincha aquí para ver en YouTube)
¿Cómo despejar X en BXB = B(X + A)? ¡Te lo explico fácil!
¿BXB = B(X + A) te parece imposible? ¡No te preocupes! En este vídeo te explico paso a paso cómo despejar X en esta ecuación matricial complicada de forma clara y sencilla.
Aprenderás:
– Cómo aplicar propiedades de matrices
– Qué hacer cuando X está entre dos matrices
– Un truco para resolverla sin errores
Ideal para Bachillerato, Universidad y preparación de EBAU/PAU
(pincha aquí para ver en YouTube)
Curso de Matrices desde Cero | Teoría + Ejercicios Resueltos (Bachillerato y Universidad)
Bienvenidos al Curso Completo de Matrices de Bego Profe
En este curso aprenderás todo lo necesario sobre matrices: desde los conceptos básicos hasta ejercicios más avanzados, siempre explicado paso a paso y con ejemplos resueltos.
Contenido del curso:
– Definición y tipos de matrices
– Operaciones con matrices
– Rango de una matriz
– Matriz inversa (Método de Gauss – Jordan)
– Matriz ortogonal
– Identidad notable e igualdad de matrices
Este curso está diseñado para estudiantes de Bachillerato, Universidad y oposiciones que quieran dominar las matrices sin ansiedad y con una explicación clara y sencilla.
Qué encontrarás en este curso:
– Teoría explicada de manera simple
– Ejercicios resueltos paso a paso
– Consejos prácticos para no cometer errores
– Ejemplos similares a los de examen